| > |
![restart; 1; with(plots); -1; with(LinearAlgebra); -1; with(Student[MultivariateCalculus]); -1](images/imitation-triangle_1.gif) |
Number of throats
| > |
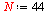 |
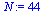 |
(1) |
Get Data and generate random throats
| > |
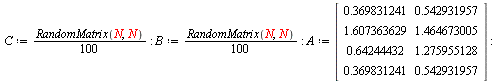 |
| > |
![gr[3] := polygonplot(convert(A, 'listlist'), axes = boxed, color =](images/imitation-triangle_5.gif) |
| > |
![gr[4] := pointplot([seq(seq([`*`(max([seq(A[q, 1], q = 1 .. 3)]), `*`(`*`(`+`(1, C[i, j]), `/`(1, 2)))), `*`(max([seq(A[q, 2], q = 1 .. 3)]), `*`(`*`(`+`(1, B[i, j]), `/`(1, 2))))], i = 1 .. N), j = 1...](images/imitation-triangle_6.gif) |
View Data
| > |
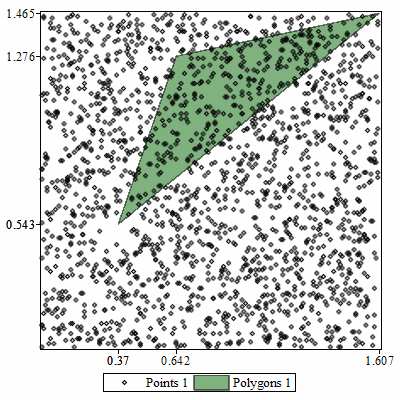
![display(gr[3], gr[4])](images/imitation-triangle_7.gif) |
Square of the triangle with vertices in the matrix A shown above . Exact result rendered by cross-product.
| > |
![M := `<,>`(`+`(A[1], `-`(A[2])), `+`(A[1], `-`(A[3]))); 1; `𝒮` := `+`(`*`(`/`(1, 2), `*`(LinearAlgebra:-Determinant(`<,>`(`+`(A[1], `-`(A[2])), `+`(A[1], `-`(A[3])))))))](images/imitation-triangle_9.gif) |
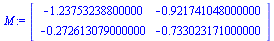 |
 |
(2) |
Getting typical Data points
| > |
![Extrema := max([seq(A[q, 1], q = 1 .. 3)]), max([seq(A[q, 2], q = 1 .. 3)])](images/imitation-triangle_12.gif) |
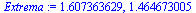 |
(3) |
| > |
![Means := [Statistics:-Mean([seq(A[q, 1], q = 1 .. 3)]), Statistics:-Mean([seq(A[q, 2], q = 1 .. 3)])]](images/imitation-triangle_14.gif) |
![[HFloat(0.8732130633333334), HFloat(1.0945200300000002)]](images/imitation-triangle_15.gif) |
(4) |
| > |
![gr[0] := pointplot(Means, symbol = cross, symbolsize = 20, color = red); -1](images/imitation-triangle_16.gif) |
Set the system by Data
| > |
![Sys := [seq(`+`(y, `-`(A[`+`(q, 1), 2]), `-`(`/`(`*`(`+`(A[q, 2], `-`(A[`+`(q, 1), 2])), `*`(`+`(x, `-`(A[`+`(q, 1), 1])))), `*`(`+`(A[q, 1], `-`(A[`+`(q, 1), 1])))))), q = 1 .. 3)]](images/imitation-triangle_17.gif) |
![[`+`(y, `-`(.267473602), `-`(`*`(.7448217573, `*`(x)))), `+`(y, `-`(1.150306561), `-`(`*`(.1955789207, `*`(x)))), `+`(y, .4514989413, `-`(`*`(2.688877488, `*`(x))))]](images/imitation-triangle_18.gif) |
(5) |
Testing is a true fitness there
| > |
![Signs := [op(eval(Sys, [x = Means[1], y = Means[2]]))]; 1; Signs := seq(`/`(`*`(Signs[q]), `*`(abs(Signs[q]))), q = 1 .. 3); 1; Signs := seq(signum(Signs[q]), q = 1 .. 3)](images/imitation-triangle_19.gif) |
| > |
![rel[0] := eval([seq(`>=`(`*`(Sys[q], `*`(Signs[q])), 0), q = 1 .. 3)], [x = Means[1], y = Means[2]]); 1; seq(evalb(rel[0][q]), q = 1 .. 3)](images/imitation-triangle_23.gif) |
![[`<=`(0, HFloat(0.17665833967075073)), `<=`(0, HFloat(0.22656859946787394)), `<=`(0, HFloat(0.8019439769245182))]](images/imitation-triangle_24.gif) |
 |
(7) |
| > |
![rel[1] := eval([seq(`>=`(`*`(Sys[q], `*`(Signs[q])), 0), q = 1 .. 3)], [x = CG[1], y = `+`(1, CG[2])]); 1; seq(evalb(rel[1][q]), q = 1 .. 3)](images/imitation-triangle_26.gif) |
![[`<=`(0, `+`(.732526398, CG[2], `-`(`*`(.7448217573, `*`(CG[1]))))), `<=`(0, `+`(.150306561, `-`(CG[2]), `*`(.1955789207, `*`(CG[1])))), `<=`(0, `+`(`-`(1.451498941), `-`(CG[2]), `*`(2.688877488, `*`(...](images/imitation-triangle_27.gif) |
![`<=`(0, `+`(.732526398, CG[2], `-`(`*`(.7448217573, `*`(CG[1]))))), `<=`(0, `+`(.150306561, `-`(CG[2]), `*`(.1955789207, `*`(CG[1])))), `<=`(0, `+`(`-`(1.451498941), `-`(CG[2]), `*`(2.688877488, `*`(C...](images/imitation-triangle_28.gif) |
(8) |
Define the bounds
| > |
![upper := rhs(isolate([seq(rhs(isolate(Sys[q], y)), q = 1 .. 3)][3] = max([seq(A[q, 2], q = 1 .. 3)]), x))](images/imitation-triangle_29.gif) |
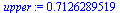 |
(9) |
| > |
![lower := rhs(isolate([seq(rhs(isolate(Sys[q], y)), q = 1 .. 3)][3] = 0, x))](images/imitation-triangle_31.gif) |
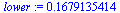 |
(10) |
Testing Rough
| > |
![[`/`(`*`(seq(int([seq(rhs(isolate(Sys[q], y)), q = 1 .. 3)][p], x = 0 .. max([seq(A[q, 2], q = 1 .. 3)])), p = 1 .. 2)), `*`(max([seq(A[q, 1], q = 1 .. 3)]), `*`(max([seq(A[q, 2], q = 1 .. 3)])))), `/...](images/imitation-triangle_33.gif) |
![[.5057559770, .8047563852, .1694437402]](images/imitation-triangle_34.gif) |
(11) |
Square of the triangle. Exact result given by multiply integral
| > |
![EQ := [seq(rhs(isolate(Sys[q], y)), q = 1 .. 3)]](images/imitation-triangle_35.gif) |
![[`+`(.267473602, `*`(.7448217573, `*`(x))), `+`(1.150306561, `*`(.1955789207, `*`(x))), `+`(`-`(.4514989413), `*`(2.688877488, `*`(x)))]](images/imitation-triangle_36.gif) |
(12) |
| > |
![S := `+`(MultiInt(1, y = EQ[1] .. EQ[3], x = A[1, 1] .. A[3, 1], output = integral), MultiInt(1, y = EQ[1] .. EQ[2], x = A[3, 1] .. A[2, 1], output = integral))](images/imitation-triangle_37.gif) |
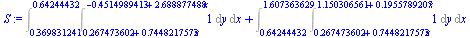 |
(13) |
| > |
![value(S), `*`(A[2, 1], `*`(A[2, 2]))](images/imitation-triangle_39.gif) |
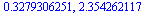 |
(14) |
Exact result given by a ratio with the rectangle square
| > |
![`/`(`*`(value(S)), `*`(A[2, 1], `*`(A[2, 2])))](images/imitation-triangle_41.gif) |
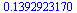 |
(15) |
Preparing result output
| > |
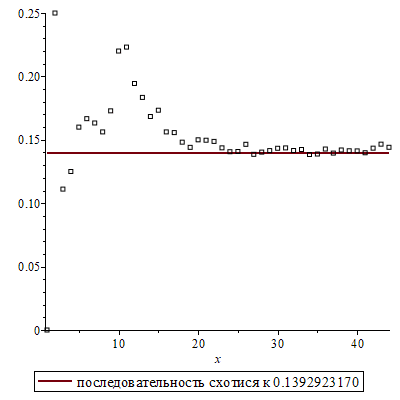
![for i by 10 to `+`(N, `-`(10)) do display(array([display(gr[0], gr[3], GR[i]), display(gr[0], gr[3], GR[`+`(i, 10)])]), scaling = constrained) end do](images/imitation-triangle_57.gif) |
| > |
![display(plot(`/`(`*`(value(S)), `*`(A[2, 1], `*`(A[2, 2]))), x = 1 .. N, legend = typeset(](images/imitation-triangle_66.gif) A;54>20B5;L=>ABL AE>B8AO : ", `/`(`*`(value(S)), `*`(A[2, 1], `*`(A[2, 2]))))), pointplot([seq(punkten[j], ..." align="center" border="0"> A;54>20B5;L=>ABL AE>B8AO : ", `/`(`*`(value(S)), `*`(A[2, 1], `*`(A[2, 2]))))), pointplot([seq(punkten[j], ..." align="center" border="0"> |
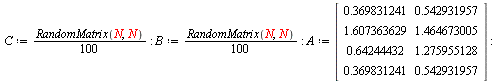
![[`/`(`*`(seq(int([seq(rhs(isolate(Sys[q], y)), q = 1 .. 3)][p], x = 0 .. max([seq(A[q, 2], q = 1 .. 3)])), p = 1 .. 2)), `*`(max([seq(A[q, 1], q = 1 .. 3)]), `*`(max([seq(A[q, 2], q = 1 .. 3)])))), `/...](images/imitation-triangle_33.gif)